Algoritma Analizinin 5N1K'sı

        Bu yazıda Algoritma analizini 5N1K sorularıyla açıklamaya çalışacağım. Bu şekilde Algoritma analizinde ne yapılmak istendiğini net bir şekilde ortaya koyacağız. Algoritma analizi ile ilgili temel kavramlarını önceki yazılarda bahsetmiştik.

Algoritma analizinde öncelikle üzerinde durulan konu, algoritmanın performansıdır.
İşte tam bu noktada sorularımızı sorup cevabını bularak algoritma analizini açıklamaya çalışacağım.


Ne Yapılmalı?
Oluşturulan algoritmanın daha iyi hale gelmesi için algoritma analizindeki temel kavramlar göz önüne alınarak kodun gerçekleştirimi yapılmalıdır. Örneğin bir arama işleminde aradığımız kaydın türüne göre algoritmayı oluşturmalıyız.
Başka bir yaklaşım olarak mümkün olduğunca az döngü yapıları kullanmak.


Neden Yapılmalı?
Algoritma analizi bilgisayar programlarının performans ve kaynak kullanımı üzerine yapılan çalışmalardır.Bilgisayar programlarında işin daha iyi nasıl gerçekleşebileceğini ele alır.

Bu doğrultuda algoritmayı analiz ederken;

-Algoritmanın performansını ölçmek
-Başka algoritmalarla karşılaştırmak
-Daha iyisi mümkün mü?
-Olabileceklerin en iyisi mi? göz önüne alırız.


Nasıl Yapılmalı?
Bir problemi bir çok algoritma ile çözmek mümkündür. Bunun için seçilecek algoritmanın performansına/verimliliğine (kullanılan hafıza ve gerçekleştirdikleri zaman) bakılarak yapılmalıdır.


Ne Zaman Yapılmalı?
Her zaman genelde performansı iyi olan algoritmaları seçmek doğru olmayabilir. Bir programın performansı genel olarak programın işletimi için gerekli olan bilgisayar zamanı ve belleğidir. Bir programın zaman karmaşıklığı (time complexity) programın işletim süresidir.


Bir programın yer karmaşıklığı (space complexity) programın işletildiği sürece gerekli olan yer miktarıdır. Bir problemin çözümünde, kullanılabilecek olan algoritmalardan en etkin olanı seçilmelidir. En kısa sürede çözüme ulasan veya en az işlem yapan algoritma tercih edilmelidir. Burada bilgisayarın yaptığı iş önemlidir. Bazı durumlarda da en az bellek harcayan algoritmanın tercih edilmesi gerekebilir.

Ayrıca, programcının yaptığı is açısından veya algoritmaların anlaşılırlıkları bakımından da algoritmalar karşılaştırılabilir. Daha kısa sürede biten bir algoritma yazmak için daha çok kod yazmak veya daha çok bellek kullanmak gerekebilir (trade-off).

Bir Algoritmanın performansı iç ve dış faktörlere bağlıdır.
Algoritma verimliliği:
-Çalıştırmak için gereken zaman
-Çalıştırmak için gereken yer(bellek alanı)

Çalışma zamanı analizi

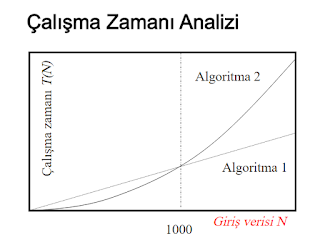
Algoritma 1:  T1(N)=1000N
Algoritma 2:  T2(N)=N^2

Büyük-O notasyonu

Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması diyebiliriz.Yada büyüme hızını gösterir de diyebiliriz.

Sık kullanılan büyüme hızları

Zaman Karmaşıklığı	Örnek
O(1)            sabit	Bağlı listeye ilk eleman olarak ekleme yapma
O(log N)      log	Sıralı bir dizide bir eleman arama
O(N)            lineer	Sıralı olmayan bir dizide eleman arama
O(Nlog N)    nlog-n	N elemanlı böl-parçala-yut yöntemiyle sıralama
O(N2)          ikinci dereceden	Bir grafikte iki düğüm arasındaki en kısa yolu bulma
O(N3)          üçüncü dereceden	Ardarda gerçekleştirilen lineer denklemler
O(2N)          üssel	Hanoi’nin Kuleleri problemi

Nerede Yapılmalı?

Programın sahte kodunun yazımında gerçekleştirilmelidir. Kodu yazarken büyük-O hesaplanmasını göz önüne alarak kodu yazmalıyız.

Büyük-O Nasıl Hesaplanır

Bir programın zaman karmaşıklığını hesaplamak 5 kural vardır.
1. Döngüler
2. İç İçe Döngüler
3.Ardışık Deyimler
4.If-then-else Deyimleri
5.Logaritmik Karmaşıklık

Kural 1: Döngüler

for(int i=0; i<=n; i++)
{
    k=k+2;
}
Bir döngünün çalışma zamanı en çok döngü içindeki deyimlerin çalışma zamanının iterasyon sayısıyla çarpılması kadardır.

Karmaşıklık  T(N) = O(N)

Kural 2: İç İçe Döngüler 

for(int i=0; i<=n; i++)
{
   for(int j=0; j<=m; j++)
   {
       k=k+1;
   }
}
İçteki analiz yapılır. Toplam zaman döngülerin çalışma sayılarının çarpımına eşittir.

Karmaşıklık   T(N) = O(N^2)

Kural 3:Ardışık Deyimler

x=x+1;
for(int y=0; y<=n; y++)
{
   m=m+1;
}

for(int i=0; i<=n; i++)
{
   for(int j=0; j<=m; j++)
   {
       k=k+1;
   }
}
Her deyimin zamanı birbirine eklenir.
Karmaşıklık   T(N) = 1+N+N^2
                       T(N) = O(N^2)

Kural 4: IF-Then-Else Deyimleri

if(i<=10)
{
   return false;
}
else
{
   for(int i=0; i<=n; i++)
{
    if(i==0)
   {
      return true;
   }
}
En kötü çalışma zamanı: test zamanına then veya else kısmındaki çalışma zamanının hangisi büyükse o kısım eklenir.

Kural 5: Logaritmik Karmaşıklık

Problemin büyüklüğünü belli oranda (genelde 1/2) azaltmak için sabit bir zaman harcanıyor ise bu algoritma O(log N)'dir.

Örnek algoritma binary search:
-Sözcüğün orta kısmına bakılır.
-Sözcük ortaya göre sağda mı solda mı kaldığı bulunur.
-Bu işlem sağ veya solda sözcük bulunana kadar tekrarlanır.

Kim Yapmalı?
Kullanılacak algoritmanın seçiminde  programı kodlayan kişi tarafından yazmak istediği kodun verimliğini düşünerek yapmalıdır.